MP313 Number Theory III, Semester 2, 1999
The lecture notes will contain enough explanations and examples to make the definitions, theorems and arguments clear. However some students will need further examples and explanations of certain points and I recommend they peruse books from the reading list below. Most of these books have lots of examples and develop the concepts in greater detail than we have time for in our short course of lectures.
Course Outline
(For an outline of what number theory is all about, see Wikipedia).
We start with a review of congruences and congruence classes, Euclid's algorithm, gcd, lcm, Euler's function, Euler-Fermat theorem, orderma, Chinese remainder theorem.
Then Pythagorean triples, polynomial congruences, primitive roots, binomial conguences, pseudoprimes and strong pseudoprimes and simple primality tests and the Shanks Giant step/Baby step and Pohlig-Helman solutions of the discrete logarithm problem.
Then we study quadratic residues and non-residues (mod p), the Legendre and Jacobi symbols, Euler's criterion, the quadratic reciprocity theorem and some consequences.
Calculating the integer part of a1/m, Thue's theorem on small solutions of ax 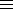 y (mod b), Serret's algorithm for p=x2+y2, Tonelli's √a (mod p) algorithm.
y (mod b), Serret's algorithm for p=x2+y2, Tonelli's √a (mod p) algorithm.
Finally, we turn to more technical topics such as continued fractions, Pell's equation, p-adic numbers.
Time does not permit us to investigate further interesting topics such as quadratic fields, lattices in 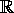 n, Minkowski's convex body theorems, the LLL algorithm, Dirichlet characters, Gaussian sums, Pólya-Vinogradov inequality, elliptic curves and the congruent number problem and the distribution of primes.
n, Minkowski's convex body theorems, the LLL algorithm, Dirichlet characters, Gaussian sums, Pólya-Vinogradov inequality, elliptic curves and the congruent number problem and the distribution of primes.
The subject contains many interesting algorithms. Students can experiment with an exact arithmetic computer program called CALC, written by the lecturer and which implements some of the algorithms met in the course.
CALC can be downloaded from the WWW.
Reference books
There are many books in the PSE and Undergraduate Libraries which touch on the subject. Here are some useful ones :
The book of Kumanduri and Romero is recommended.
- Number Theory with Computer Applications, R. Kumanduri and C. Romero, Prentice Hall 1997
- An Introduction to the Theory of Numbers, I. Niven, H.S. Zuckermann, H.L. Montgomery, (5th edition), Wiley 1991
- Elementary Number Theory and Its Applications, K.H. Rosen, (6th edition), Pearson Education 2013
- A Concise Introduction to the Theory of Numbers, A. Baker, CUP 1985
- A Course in Number Theory, 2nd Edition, H.E. Rose, OUP 1995
- A Classical Introduction to Modern Number Theory, K. Ireland and M. Rosen, (Corrected Second Printing) Graduate Text 84, Springer 1993
- Number Theory: an Introduction, D. Redmond, Pure and Applied Mathematics Series 201, CRC Press, 1996
Some Informative Number Theory Sites
Return to top of page
KRM 16th July 2019
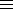 y (mod b), Serret's algorithm for p=x2+y2, Tonelli's √a (mod p) algorithm.
y (mod b), Serret's algorithm for p=x2+y2, Tonelli's √a (mod p) algorithm.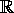 n, Minkowski's convex body theorems, the LLL algorithm, Dirichlet characters, Gaussian sums, Pólya-Vinogradov inequality, elliptic curves and the congruent number problem and the distribution of primes.
n, Minkowski's convex body theorems, the LLL algorithm, Dirichlet characters, Gaussian sums, Pólya-Vinogradov inequality, elliptic curves and the congruent number problem and the distribution of primes.