Lecture Summary, MP313 Number Theory III, Semester 2, 1999
- Lecture 1
- Revision of divisibility, congruences, congruence or residue classes, Euclid's algorithm: r0=a, r1=b, rk=rk+1qk+1+rk+2, 0 < rk+2 <rk+1 and gcd(a,b), the sequences sk,tk, where rk=ska+tkb, inverse of b (mod m), reduced residue class.
- Lecture 2
- Euler's phi function, complete set (mod m), the complete set ak+b, gcd(a,m)=1, reduced set (mod m), the reduced set kb, gcd(b,m)=1, solving a linear congruence ax
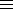 b (mod m), multiplicativity of Euler's function, formula for Euler's function.
b (mod m), multiplicativity of Euler's function, formula for Euler's function.
- Lecture 3
- Euler-Fermat theorem, summing Euler's function over the divisors of n, two proofs - one involving partitioning, the other via the multiplicative function obtained by summing a given one over the divisors of n, d(n), sigma(n) and perfect numbers.
- Lecture 4
- Characterisation of even perfect numbers, the Möbius function, summing the Möbius function over the divisors of n (two proofs), the Möbius inversion formula, application to formula for Euler's function, Chinese remainder theorem, 1-1 correspondence between residue classes mod m and the cartesian product of the residue classes mod mi, where m=m1...mt is a product of pairwise relatively prime moduli, the restriction of this to the group of reduced residue classes (mod m),
- Lecture 5
- Solving polynomial congruences (mod m) - using the Chinese remainder theorem to reduce the problem to m=pn, further reduction to m=p.
- Lecture 6
- ordma, prime divisors of x2n+1, calculating ordma efficiently, primitive root (mod m), primitive roots (mod p) exist.
- Lecture 7
- A primitive root/primality test, Pepin's test for primality of Fn=22n+1, Pocklington's test, Proth's theorem on the primality of n=h2m+1, h < 2m, primitive roots (mod pn) and (mod 2pn), primitive roots exist (mod m) if and only if m=2, 4, pn and 2pn, binomial congruences, solubility of xn
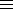 a (mod p).
a (mod p).
- Lecture 8
- The Legendre symbol
 , Euler's criterion, trapdoor functions, Shanks' baby steps-giant steps algorithm, quadratic residues and non-residues (mod p), evaluation of
, Euler's criterion, trapdoor functions, Shanks' baby steps-giant steps algorithm, quadratic residues and non-residues (mod p), evaluation of  , solving x2
, solving x2 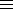 -1 (mod p) if p=4n+1.
-1 (mod p) if p=4n+1.
- Lecture 9
- Multiplicativity of the Legendre symbol, np (the least quadratic nonresidue mod p), np is prime,
 , Blum numbers pq, quadratic residues (mod pq), principal square roots (mod pq), random bit strings and bitwise encryption.
, Blum numbers pq, quadratic residues (mod pq), principal square roots (mod pq), random bit strings and bitwise encryption.
- Lecture 10
- Gauss' lemma, evaluation of
 , quadratic reciprocity.
, quadratic reciprocity.
- Lecture 11
- Applications of quadratic reciprocity: Evaluation of
 , primitive roots mod special primes, prime factors of 22n+1, converse of Pepin's theorem, evaluating the Legendre symbol, bad way:- factoring, good way:- Jacobi symbol
, primitive roots mod special primes, prime factors of 22n+1, converse of Pepin's theorem, evaluating the Legendre symbol, bad way:- factoring, good way:- Jacobi symbol  .
.
- Lecture 12
- Reduced residues (mod 2n), Tonelli's √d (mod p) algorithm, calculating the integer part of a1/m, testing for perfect powers.
- Lecture 13
- Euclid's algorithm revisited, Thue's theorem on small solutions of ax
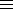 y (mod b), Serret's algorithm for p=x2+y2, uniqueness of such a representation, extension to p=x2+ny2, n=2,3,5.
y (mod b), Serret's algorithm for p=x2+y2, uniqueness of such a representation, extension to p=x2+ny2, n=2,3,5.
- Lecture 14
- Pseudoprimes and strong pseudoprimes, Lucas-Lehmer test for primality of 2p-1.
- Lecture 15
- Continuation of Lucas-Lehmer, finite simple continued fractions, 2 x 2 matrix notation.
- Lecture 16
- Partial quotients, convergents pn/qn, using Euclid's
algorithm to find the simple continued fraction of a/b, uniqueness of the partial quotients, nested sequence property of the convergents, infinite simple continued fractions, nth complete quotient.
- Lecture 17
- Irrationality of an infinite simple continued fraction, finding the simple continued fraction of an irrational, [1,1,...] and [1,2,1,2,...],quadratic irrationals, reduced quadratic irrationals, an algorithm for finding the simple continued fraction of a quadratic irrational.
- Lecture 18
- Justification of the previous algorithm, purely periodic simple continued fractions represent reduced quadratic irrationals and conversely, simple continued fraction of d1/2, d rational, periodic simple continued fractions represent quadratic irrationals and conversely.
- Lecture 19
- Pell's equations x2-dy2=1, x2-dy2=±1 and associated multiplicative groups U and V, η and η0, (the least elements > 1 of U, V respectively), U={±η n | n an integer}, V={±η0 n | n an integer}, η02=η if x2-dy2= -1 has a solution.
- Lecture 20
- Finding η0 from the simple continued fraction for √d, the equation x2-dy2=±4, the associated multiplicative group W, and least element η1 > 1, x2-py2=-1 is soluble if p=4n+1 is prime, definition of p-adic integers in terms of coherent sequences, addition and multiplication of p-adic integers.
- Lecture 21
 contains all rationals of the form a/b with p not dividing b, p-adic units, px=0 implies x=0, nx=0 implies n=0 or x=0 if n is an integer, every nonzero p-adic integer has the form x=pmy, m
contains all rationals of the form a/b with p not dividing b, p-adic units, px=0 implies x=0, nx=0 implies n=0 or x=0 if n is an integer, every nonzero p-adic integer has the form x=pmy, m  0, y a unit,
0, y a unit,  is an integral domain,
is an integral domain,  , the field of p-adic numbers.
, the field of p-adic numbers.
- Lecture 22
- Every nonzero p-adic number has the form pnu, u a unit, p-adic value |x|p, limits, canonical series expansion a0+a1p + ··· of a p-adic integer, Cauchy sequences, ie. an+1 - an tends to zero, Cauchy sequences are bounded, completeness of the p-adic numbers.
- Lecture 23
- Pointed out that Serret's algorithm gives rk-12 - 2 tk-12=p if p=8n ± 1, completed proof of completeness, Hensel's lemma, versions 1,2,3. Application to square roots in
 .
.
- Lecture 24
- Example of 2-adic expansion arising from the 3x+1 mapping, compactness of
 , canonical p-adic expansion of a rational number and its periodic nature, the binomial series, example of (1+7/9)1/2 = -4/3 in
, canonical p-adic expansion of a rational number and its periodic nature, the binomial series, example of (1+7/9)1/2 = -4/3 in  , p=7.
, p=7.
- Lecture 25
- Strassman's theorem, further study.
Pages produced by the ASRAD product SLIDEZ
KRM 18th January 2002
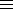 b (mod m), multiplicativity of Euler's function, formula for Euler's function.
b (mod m), multiplicativity of Euler's function, formula for Euler's function.
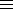 a (mod p).
a (mod p).
 , Euler's criterion, trapdoor functions, Shanks' baby steps-giant steps algorithm, quadratic residues and non-residues (mod p), evaluation of
, Euler's criterion, trapdoor functions, Shanks' baby steps-giant steps algorithm, quadratic residues and non-residues (mod p), evaluation of  , solving x2
, solving x2 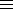 -1 (mod p) if p=4n+1.
-1 (mod p) if p=4n+1.
 , Blum numbers pq, quadratic residues (mod pq), principal square roots (mod pq), random bit strings and bitwise encryption.
, Blum numbers pq, quadratic residues (mod pq), principal square roots (mod pq), random bit strings and bitwise encryption.
 , quadratic reciprocity.
, quadratic reciprocity.
 , primitive roots mod special primes, prime factors of 22n+1, converse of Pepin's theorem, evaluating the Legendre symbol, bad way:- factoring, good way:- Jacobi symbol
, primitive roots mod special primes, prime factors of 22n+1, converse of Pepin's theorem, evaluating the Legendre symbol, bad way:- factoring, good way:- Jacobi symbol  .
.
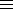 y (mod b), Serret's algorithm for p=x2+y2, uniqueness of such a representation, extension to p=x2+ny2, n=2,3,5.
y (mod b), Serret's algorithm for p=x2+y2, uniqueness of such a representation, extension to p=x2+ny2, n=2,3,5.
 contains all rationals of the form a/b with p not dividing b, p-adic units, px=0 implies x=0, nx=0 implies n=0 or x=0 if n is an integer, every nonzero p-adic integer has the form x=pmy, m
contains all rationals of the form a/b with p not dividing b, p-adic units, px=0 implies x=0, nx=0 implies n=0 or x=0 if n is an integer, every nonzero p-adic integer has the form x=pmy, m  0, y a unit,
0, y a unit,  is an integral domain,
is an integral domain,  , the field of p-adic numbers.
, the field of p-adic numbers.
 .
.
 , canonical p-adic expansion of a rational number and its periodic nature, the binomial series, example of (1+7/9)1/2 = -4/3 in
, canonical p-adic expansion of a rational number and its periodic nature, the binomial series, example of (1+7/9)1/2 = -4/3 in  , p=7.
, p=7.