Finding the continued fraction of e^(p/q)

Finding the continued fraction of e^p/q

The continued fraction expansions for e^1/k and e^2/k (k odd) are well known, namely:

However there is no known formula for the partial quotients of the continued fraction expansion of e³, or more generally e^p/q, with p distinct from 1,2 and gcd(p,q)=1.
Here are the first 250,000 partial quotients of e³ and here is the table size-sorted. The largest partial quotient is a₁₉₆₄₄₀ = 546341.

We perform the algorithm of J.L. Davison, An algorithm for the continued fraction of e^p/m, Proceedings of the Eighth Manitoba Conference on Numerical Mathematics and Computing (Univ. Manitoba, Winnipeg, 1978), 169-179, Congress. Numer., XXII, Utilitas Math.

The starting point is a result of R.F.C. Walters in Alternate derivation of some regular continued fractions, J. Austr. Math. Soc 8 (1968), 205-212): If

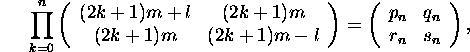
then p_n/r_n and q_n/s_n → e^l/m.

We first find the least n=n* such that p_n, q_n, r_n, s_n are non-negative and repeatedly apply Raney's factorisation for n*≤ k ≤ n*+N, as in Davison's example in §3.
The number (count) of partial quotients of e^p/q found is returned.
We cannot predict the value of count, but it becomes positive for sufficiently large N.
We restrict taking p/q no greater than 14, because of the time taken to compute a₀ for larger values of p/q.

This is a BCMATH translation of a BC program.
A faster C version is available.

Inside the program, p and q are replaced by p/gcd(p,q) and q/gcd(p,q).

Last modified 19th August 2017
Return to main page

Finding the continued fraction of ep/q

Finding the continued fraction of e^p/q