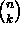Prime-power factorization of binomial coefficients

For each prime p ≤ n, we compute the power of pe dividing the binomial coefficient .
The program uses the fact that e=E(n,k,p) is the number of borrows in the subtraction n – k in base p for each prime p ≤ n.
Here n > k > 0.

(See P. Goetgheluck, Computing Binomial Coefficients, American Math. Monthly 94 (1987) 360-365.
Note that Goetgheluck's statement on p. 364 that E=1, if n – k < p ≤ n, assumes k ≤ n/2.)

The algorithm computes the number B(n,k) of borrows in the subtraction n - k in base p.

Enter n (17863 ≥ n > 1):
Enter k (n > k > 0):

The bc code I use is:

define E(n,k,p){
auto e,f,r,a,b
e=0;r=0
if(k>n/2){
  k=n-k
}
if(p>n-k){
  return (1)
}
if(p>n/2){
  return (0)
}
f=sqrt(n)
if(p>f){
	if(n%p < k%p){
	    return(1)
        }else{
	    return(0)
        }
}
while(n){
   a=n%p; n=n/p
   b=k%p+r; k=k/p
   if(a<b){
     e=e+1
     r=1
   }else{
     r=0
   }
}
return(e)
}
Last modified 27th February 2004
Return to main page